My research focuses on using a combination of astronomy, statistics, and computer science to understand the how galaxies like our own Milky Way form, behave, and evolve over time. This often involves working with massive datasets that include observations of billions of stars and galaxies across the electromagnetic spectrum, plus a lot of collaboration with other researchers at the University of Toronto and beyond! Some information on a few areas I am working on can be found below.
I am also a member of the SDSS-V, DESI, H3, and S5 collaborations. If you're interested in working with me on a short-term or long-term project, please don't hesitate to reach out! My contact information can be found on the Home page.
Milky Way
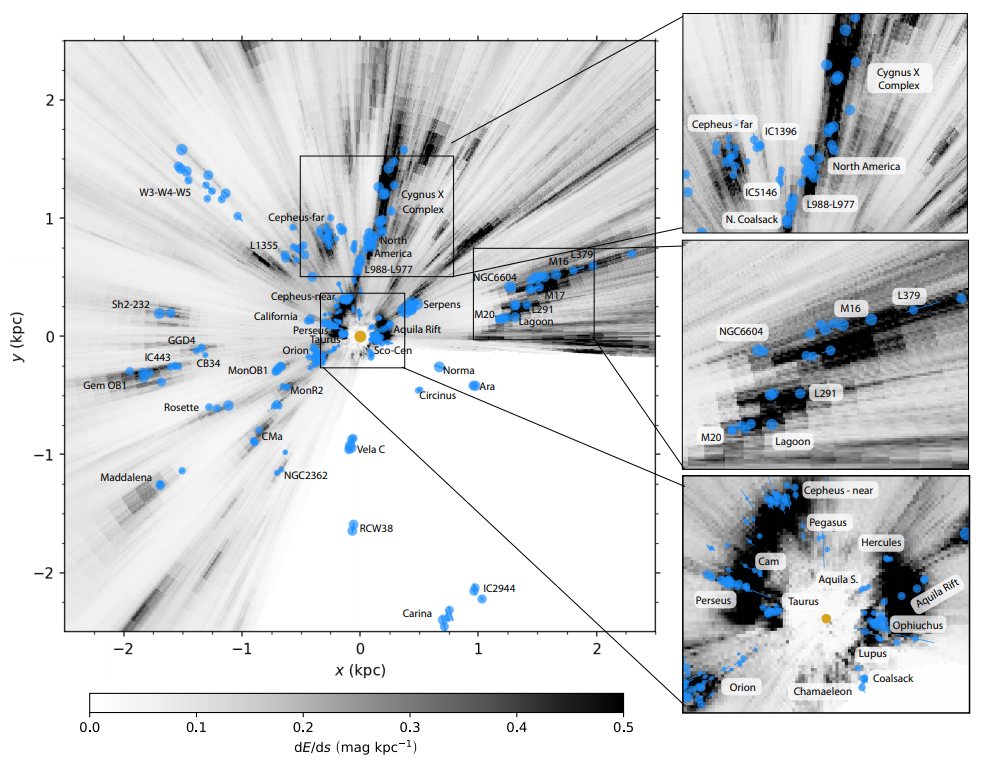
Our own Milky Way Galaxy is comprised of roughly 200 billion stars. These stars trace Galactic structure and serve as records of the formation history of the Galaxy. Studying them, however, is challenging because we can't tell, e.g., how old they are or how far away they are from us from just images of the sky. This is made even more difficult because the Galaxy is also filled with cosmic dust, which blocks and ''reddens'' the light from many of these stars. We also know many stars are born together in clusters from clouds of dense molecular gas in a complicated, hierarchical process.
Studying Galactic structure, dynamics, and evolution with modern astronomical datasets requires integrating observations of all of these features (stars, dust, gas, etc.) from many different datasets and at many different scales. I am interested in combining these data with theoretical and data-driven models to create sophisticated models of the Milky Way such as 3-D dust maps.
Stellar Populations
In addition to serving as useful tracers of Galactic structure, stars are also natural laboratories for testing fundamental physics. Modeling their evolution and internal structure requires a combination of nuclear physics, radiative transfer, magnetohydrodynamics, and more. Their evolution can also be sensitive to additional processes such as chemical composition, magnetic dynamos, and interactions with binary companions. Studying them therefore provides a window into a whole suite of interesting physical processes that are important for understanding how stars like our Sun came to be the way they are today.
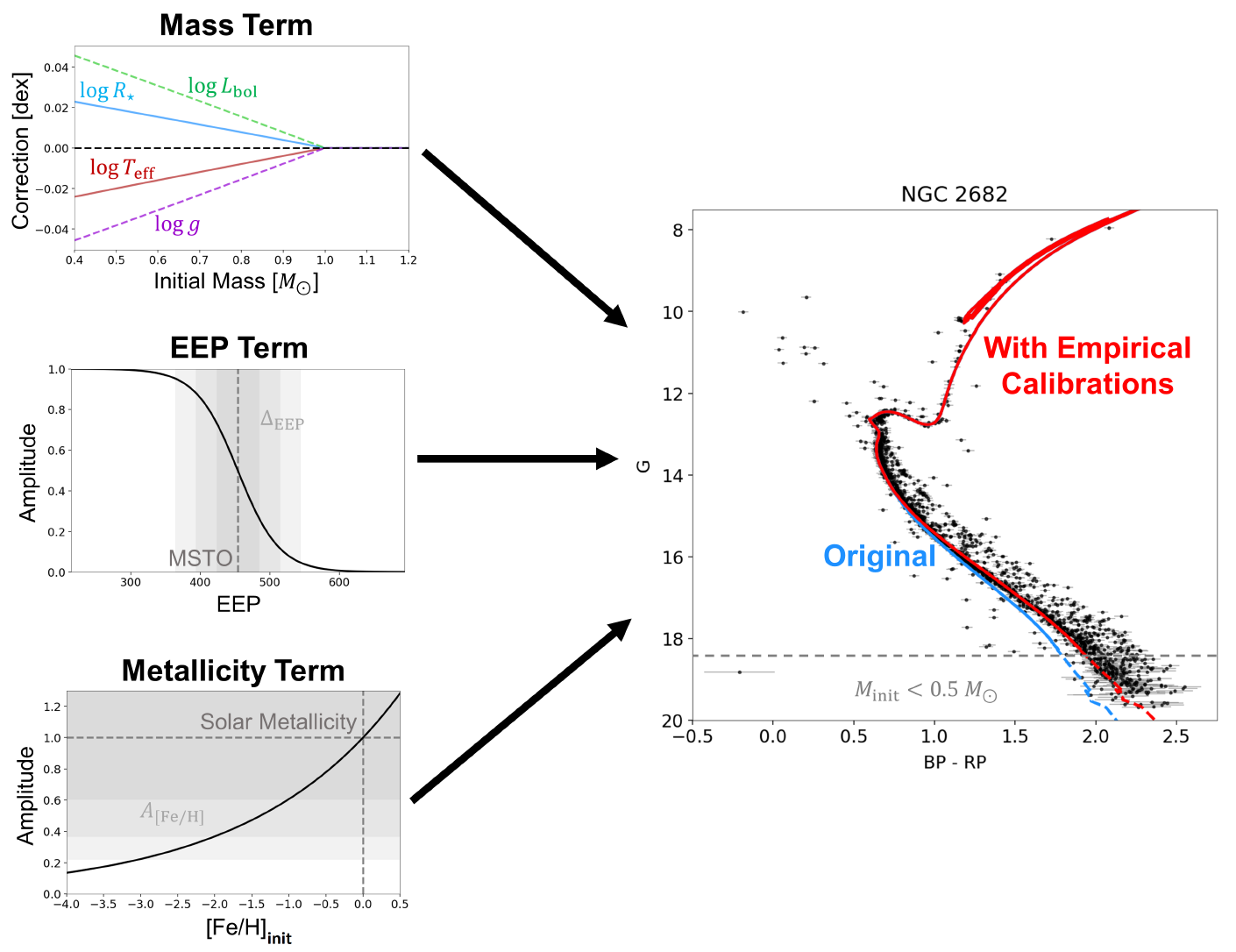
Over the last decade, imaging, spectroscopic, and time-series data has become available for stellar populations ranging from the tens of thousands to the billions. I am interested in using these data to investigate stellar behavior using methods such as asteroseismology and gyrochronology, upon which we can test and improve current state-of-the-art theoretical stellar models, and build new, empirical stellar libraries.
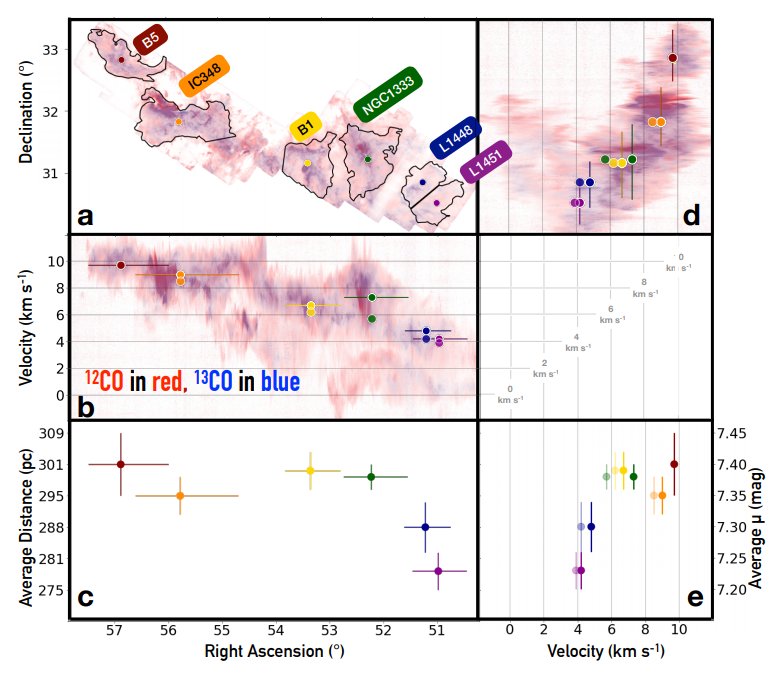
More recently, I have also become interested in developing new methods to study star clusters. Stars are often born in large groups at around the same time from a single parent molecular cloud, which means that they share many common properties. However, over time these star clusters dissipate into stellar streams and eventually completely dissolve as individual stars migrate to new locations throughout the Galaxy. Looking at surviving star clusters today (both younger open clusters and older globular clusters) therefore can not only give us insights into how stars are born and how they evolve, but also serve as a fossil record for the evolutionary history of our Galaxy.
Galaxy Evolution
The story of how galaxies form and evolve is complex and involves many moving pieces. Observations suggest galaxies are formed hierarchically through the merger of many smaller galaxies throughout the course of their lifetimes, and their evolution is a complex interplay of secular processes involving ongoing star formation and gas physics as well as catastrophic processes such as mergers with neighboring galaxies and feedback from their central supermassive black holes that can rapidly "quench" star formation. This leads to an extraordinary diversity of galaxies with varied assembly histories and physical properties.
To understand the details of how galaxies evolve, we need to observe large samples of galaxies across the electromagnetic spectrum in order to constrain their formation and evolutionary histories. Astronomers have had difficulty keeping pace with the increasing quantity and quality of data from large surveys, which now include images taken at many wavelengths, 1-D and 2-D spectroscopy, and spatially-resolved IFU data. These often contain complementary information but are challenging to model. I am interested in developing techniques and tools designed to model these data to learn more about the underlying galaxy and stellar populations, especially with new data from the James Webb Space Telescope.
Along the same lines, I am interested in using galaxies as external laboratories to study our own Galaxy. Many of the ingredients that go into modelling other galaxies include things such as dust properties, stellar populations, and more, allowing there to be a natural feedback loop between what we can learn from other galaxies and what our own Galaxy can teach us about how all these pieces fit together. This also holds true for large star clusters, which we also can observe both in nearby galaxies such as Andromeda as well as extremely faraway galaxies. Figuring out what parts of the Milky Way we can learn from to understand other galaxies better, what parts of other galaxies we can use to understand our own Galaxy, and how we should even be trying to make those comparisons often entails developing new approaches to work with an exciting mix of observational results, physical theory, and numerical simulations.
Data Integration
Modern science has entered the era of "big data", with large datasets commonly available across a host of scientific domains from genomics to economics to astronomy. These datasets often overlap with each other while probing complementary sets of information, and so jointly modeling them often enables us to draw better statistical inferences.
While straightforward in theory, this type of "data integration" in astronomy is often difficult since many of these datasets possess widely different characteristics, trace different sub-populations, depend on different physical processes, and often only partially overlap. I am interested in developing methods to deal with these types of data to tackle many of the exciting problems described above, as well as to address these issues across the sciences more generally.
Machine Learning
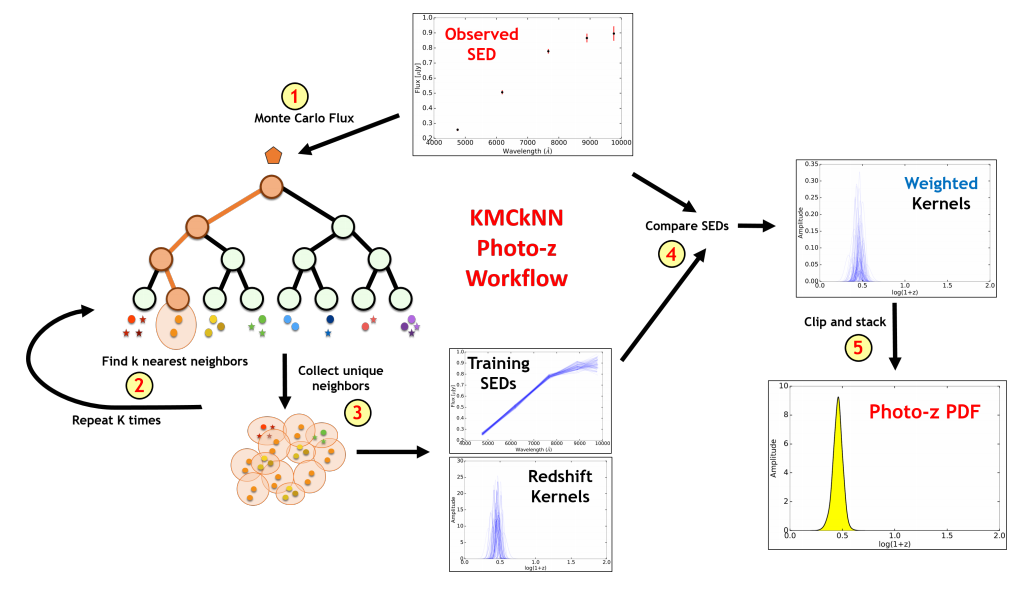
Analyzing large datasets has increasingly become the domain of machine learning methods. However, these methods tend to have difficulty deriving estimates of the uncertainty and reliability of their predictions and can often be difficult to interpret. While performing statistical inference with interpretable models can help to address these concerns, many methods are often prohibitively slow and therefore limited to small datasets.
In order to address these concerns, I am interested in combining elements of machine learning and statistical modeling to develop quick yet robust approaches for "scalable" inference and "probabilistic" machine learning that can be applied to large datasets. I am especially keen on incorporating things such as fundamental physics (e.g., doppler shifts), geometry (e.g., symmetries), and observational effects (e.g., noise, censoring) into this process. I also study how to use these methods to facilitate data-driven discovery, and how to make them more robust to both natural outliers and adversarial attacks.
Sampling Methods
Much of science involves using data to test, constrain, and/or rule out various models that represent our current understanding of how we think things work. These models are often complex, involving on many parameters and requiring lots of computational effort to generate. The constraints on these parameters given our data (and possibly prior beliefs) are often unknown (and can sometimes be multi-modal), requiring the use of numerical techniques to estimate them.
One class of techniques for estimating these constraints relies on generating random samples from the distribution via computationally tractable numerical simulation. These are known as a "Monte Carlo" approaches, and include methods such as Markov Chain Monte Carlo that are widely used throughout the sciences. I am interested in developing efficient sampling strategies for general problems as well as for particular applications in astronomy. I am especially interested in methods that can scale efficiently to many parameters, can perform well on complex, multi-modal distributions, and/or that can be used to help differentiate between possible competing models.